
James Brown - Software Engineer

Engine: AIE Open GL Graphics Engine, Custom Physics Engine
Language Used: C++
Primary Role: Physics Engine Programmer
Additional Role: General Gameplay
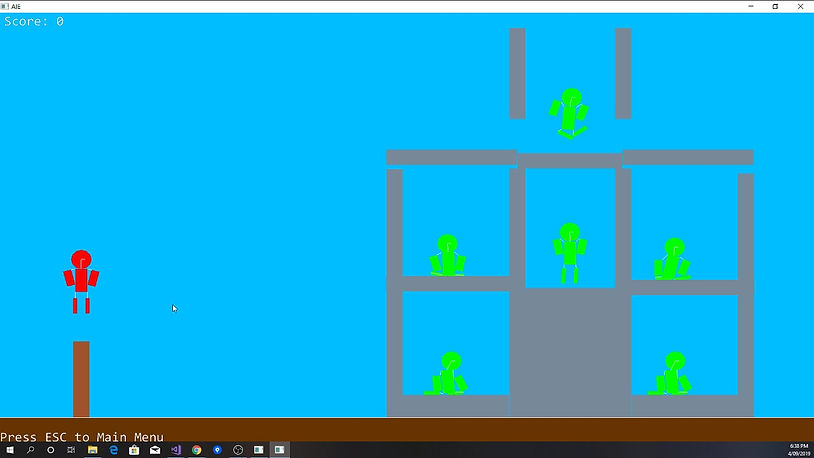
Ragdoll Extravaganza is a project I developed as part of a second year assignment at the Academy of Interactive Entertainment, where I had to develop a custom physics engine that simulates Newton's laws of motion, springs, and static and dynamic rigid bodies. I developed the engine and game over the course of four weeks and decided to show off the engine with a recreation of Angry Birds, where players are instead tasked to shoot towers down with a wacky ragdoll constructed with primitive shapes that are connected by tight springs.

Ragdoll System
Through the combination of primitive shapes and springs I was able to craft a simplistic ragdoll system that brings a more lively and comedic tone to the main game. Each limb are connected via a tightened spring that are locked to joint positions that get calculated upon creation and are set up to remain clamped to a specified area despite the scale of the limb the joint is attached to (i.e. shoulder joints will always remain in the top corners of the torso, the head joint remains centered, etc). Additionally, I applied weight across the ragdoll for a realistic gravitational affect on the body which i accomplished by researching what the average distribution of mass in the male human body is and distributed my current weight at the time of 81kg accordingly across the ragdoll.
Code Sample

Ragdoll Header
Ragdoll Source

Physics Scene System
I implemented a complicated system that handles the base logic of the physics engine which involves checking and resolving collisions between static and dynamic rigid bodies. As noticed in the sample provided below, the system utilizes an array of bool function pointers that take two physics objects as its parameters. The specified function gets called upon check collision where an index is determined based on adding the colliding shapes ID's and scaling it by number of collider variations. However, while this method works it is easily prone to logic errors as it requires that the functions in the array be ordered in a particular way which can unnecessarily complicate things and cause undesired behaviours when adding new collider types. A more simplistic and readable way of going about this could be to directly check the two comparing objects collider types and call the according function instead.
Continuing, upon entering the chosen function the two objects being checked are dynamically cast to their appropriate colliders to utilize the correct collision detection algorithms such as BoxOBB, BoxABB, Circles and Planes to test if both objects are penetrating each others surfaces. If they are, the appropriate contact forces are then applied to both objects to resolve the collision.
Code Sample
Physics Scene Header
Physics Scene Source

Rigidbody System
The rigidbody system is the most pivotal system in the engine as it not only serves as a base type for collider classes (e.g. BoxOBB, BoxABB, etc), it also handles the resolution of collisions between itself and other bodies in scene while also containing references to its own current mass, position, orientation, velocity and scale. Furthermore, the formula 𝑗 = (−(1 + 𝑒)𝑉𝑟𝑒𝑙 ∙ 𝑛) / (𝑛 ∙ 𝑛( 1 𝑀𝐴 + 1 𝑀𝐵 )) is utilized to calculate a resolving force vector that is applied to both bodies with the force vector being inversed for itself in order to simulate an equal and opposite reaction.
Code Sample
Rigidbody Header
Rigidbody Source

Spring System
This system utilizes Hookes Law (F = -kx) to determine how much force to apply to two points that are connected via a spring, such that a spring at rest will exert no force, stretched will draw both points to pull towards each other and compressed will cause both points to push away from each other. Springs can also be damped (F = -kx - bv) to prevent the springs from oscillating forever and never losing energy.
Code Sample

Spring Header
Spring Source

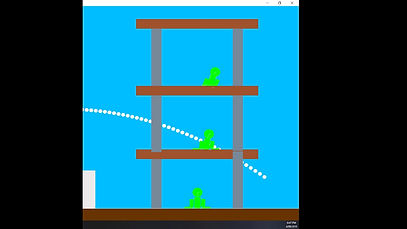
Calculating Trajectory Curve
A key feature of the physics engine demo is the ability to determine the predicted trajectory of the ragdoll in order to assist players with aiming at the enemy structure. This is accomplished through the use of the third kinematic formula (∆𝑥 = 𝑣0𝑡 + 1/2 𝑎𝑡^2) where we can determine how far an object has moved without knowing its final velocity. As seen in the sample below, this is simply accomplished by stepping forward in delta time by 0.5 intervals 40 times and then using the formula to calculate the predicted position per interval while also drawing a circle at the calculated position to display the predicted trajectory. However, the predicted trajectory can sometimes be off slightly as I am unable to account for the forces applied to the ragdoll by the springs while in flight, and discrepancies between the analytic solution and the timestepped behaviour of the physics engine.
Code Sample

Physics Engine Source